This writeup presents a solution to the SSSGX Wallet stage of the 2020 Ledger Donjon’s CTF. It showcases a solution using a kind of generic method to exploit the issues that we are facing in this challenge, which can basically be reduced to solving a linear system in the vector space \(\{0,1\}^N\).

We will first describe the challenge, then the generic problem to solve, the vulnerability to exploit, and finally how to solve the challenge using Sage and DragonFFI!

The full code of this solution is available on Github.

Introduction

For this challenge, we had access to a web-browser based wallet service (and its source code), on which we can create or restore accounts, and digitally sign messages with that account.

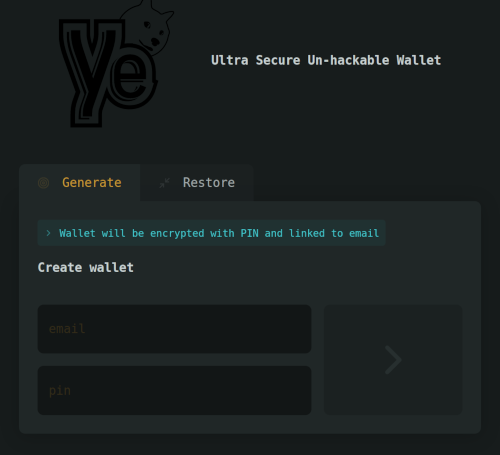
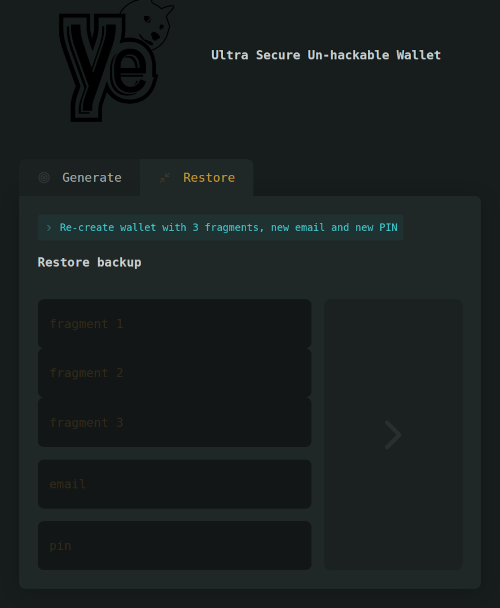
This system also has the particularity of allowing the user to split the secret associated to his account in three “shares”, and to send two of them to two other persons, so that he’ll be able to recover his account if the three shares are put back together.

In the challenge’s data, we are also given a copy of the local storage SQLite database of a browser that has been using this service. Indeed, once an account has been created on this platform, we can see that a “backup” local storage entry appears, with information linked to our account.

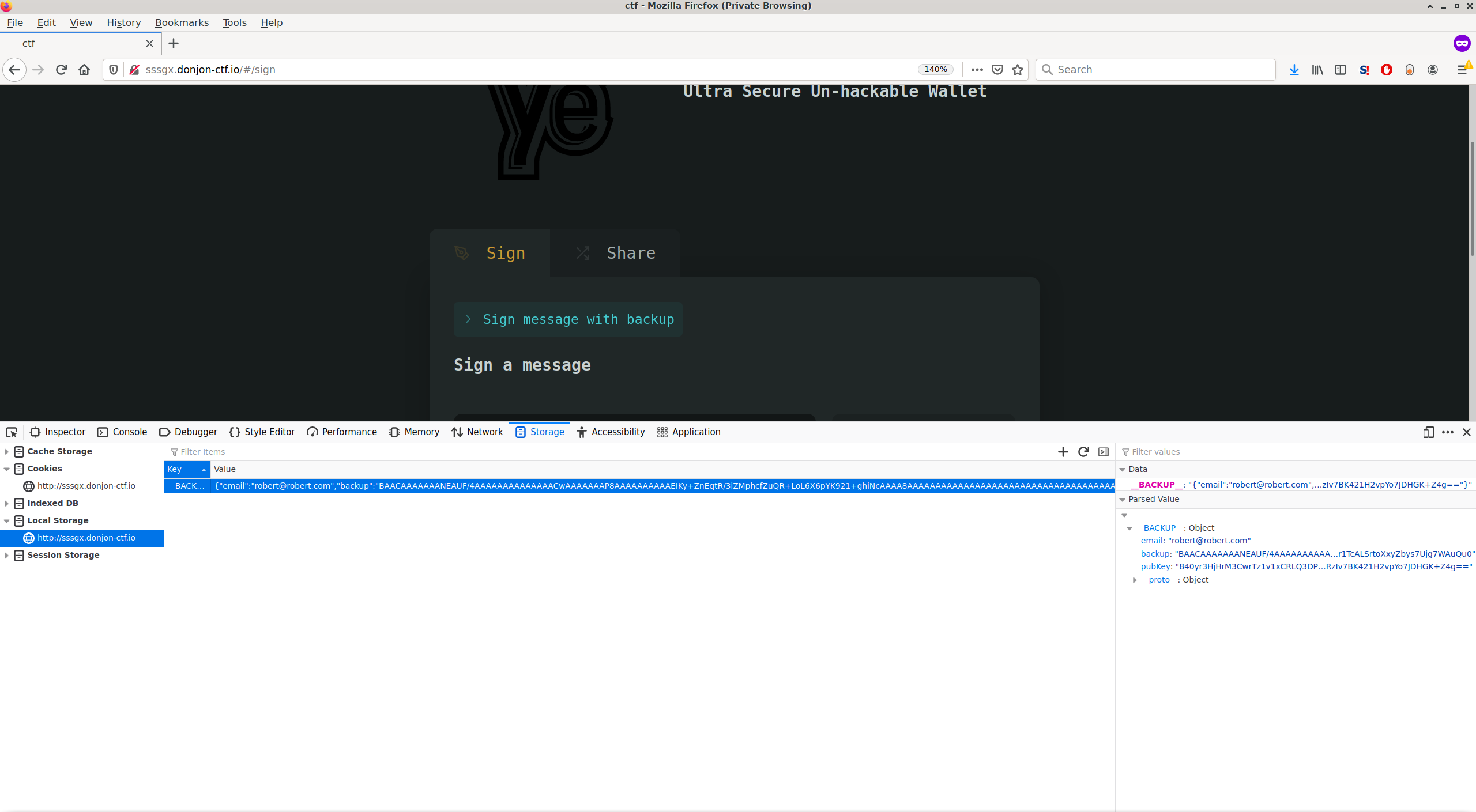
The goal of the challenge is to retrieve the secret associated to that account.

As we have the source code, let’s take a look at it to understand what are these data, especially the backup field.

Service architecture

The service has actually a quite interesting Intel SGX-based architecture. What happens when an account is created is:

• a random 32-bytes secret \(S\) is generated in an SGX container. It is later used to sign messages using ECDSA
• this secret is encrypted and authenticated in the very same container, alongside with the email information and the users’ PIN
• the result is sent back to the user that stores it in its browser local storage

When a user asks to sign a message, he has to enter its PIN. The complete request, containing the message, the PIN and the encrypted backup, is forwarded to the SGX container, which:

• decrypts the backup
• verifies the users’ PIN
• signs the message

The signature is then sent back to the user.

If the user wants to send its shares to two of his friends, he just send his encrypted backup alongside with the two recipients’ mail address. This is the only API we can use with the backup that have been provided in the challenge, because the PIN isn’t requested and checked here.

Figuring out the problem to solve

What data do we have

It looks like solving this challenge would imply using the two shares that the server is willing to send us. Using the SQLite database we are provided with, we inject it into the browser of our choice, and ask the interface to send the shares to two email addresses we control:

For the sake of history, the two resulting shares are available in the repository of the solution.

Now, let’s go back to the code and look at the “data flow” between our victim’s secret (what we are looking for) and the two shares we have. Given the name of the challenge, we are expecting to find some sharing scheme, like the Shamir’s Secret Sharing (SSS) one.

What function computes them

We are interested in isolating the function that computes these two shares from the original secret.

From the code, in the file src/wallet/libwallet/Enclave/Enclave.cpp, the function share_user_seed looks interesting. It is indeed declared as a “public endpoint” of the enclave in src/wallet/libwallet/Enclave/Enclave.edl, is wrapped in the function wallet_share_seed, which itself is called by the Node.js server by the /share public REST API, all through of bunch of bindings we don’t describe here. The shares we got by email have thus been generated by the share_user_seed function, which looks like this (stripped down for readability):

sgx_status_t share_user_seed(share_t contact_shares[3], const uint8_t *blob, uint32_t blob_size, const char *password, const char *email1, const char *email2) {
    sgx_status_t status;
    sss_Share shares[3];
    user_data_t user_data;
    uint8_t entropy[16];

    // No need to check the password, as one share will always be sent to the owner email address.
    // We can assume access to the mail account is enough.
    (void) password;

    unseal_user_data(blob, blob_size, &user_data);
    sgx_read_rand(entropy, sizeof(entropy));
    randominit(entropy, sizeof(entropy));

    uint8_t msg[sss_MLEN] = {0};
    memcpy(msg, &user_data.key, sizeof(user_data.key));
    sss_create_shares(shares, msg, 3, 3); 

    [...]
    for (int i = 0; i < 3; i++) {
        memcpy(contact_shares[i].data, shares[i], sss_SHARE_LEN);
    }   
    return SGX_SUCCESS;
}

It is indeed using Shamir’s Secret Sharing (SSS) protocol, splitting the secret in three shares and requiring the three of them to recover the secret. The core function that creates these shares is sss_create_shares, which is from the sss library by Daan Sprenkels. This function takes as input the user’s secret key (which we are interested in), and returns three shares. Given these three shares, it is possible to do the inverse operation, i.e. recompute the original user’s secret. As a reminder, we only have two of these shares.

Shamir’s Secret Sharing, and its implementation in sss

Shamir’s Secret Sharing scheme is a secret sharing scheme. The goal is to share a secret between \(n\) participants, and require at least \(k\) participants to retrieve it.

SSS implements this using polynomials. This is best described by the Wikipedia’s article on the matter:

The essential idea of Adi Shamir’s threshold scheme is that 2 points are sufficient to define a line, 3 points are sufficient to define a parabola, 4 points to define a cubic curve and so forth. That is, it takes \(k\) points to define a polynomial of degree \(k-1\).

The degree of the polynomial \(P\) will thus be \(k-1\). We embed the secret into this polynomial, for instance by setting its constant coefficient \(P(0)\) to the secret, and the rest to random values. We then evaluate this polynomial in \(N\) points, and share a different \((i,P(i))\) pair with each of the \(K\) participants. If we know \(K\) shares, we can retrieve the full polynomial using interpolation, and hence retrieve the secret.

In the case of our challenge, for one secret, the sss library uses 32 polynomials with coefficients in the \(GF(2^8)\) space (which are themselves polynomials). According to the source code of the library, multiplication in \(GF(2^8)\) is reduced by this polynom: \(x^8 + x^4 + x^3 + x + 1\). This means that, for this challenge, shares are polynomials, as well as coefficients of the Shamir polynomial.

Moreover, for one secret, it uses 32 Shamir polynomials, because one Shamir polynomial with coefficients in \(GF(2^8)\) can only store a secret of one byte (aka 8 bits). Indeed, as we will see below, the library encrypts the secret with a random 32-byte encryption key (which then is the actual shared secret), hence the 32 polynomials.

Bitslicing

In order to make computations with these 32 polynomials efficient, the library uses a technique called bitslicing. Instead of working with 32x8-bit integers (each integer representing a polynomial over \(GF(2^8)\), it works with 8x32-bit integers. Each 32-bit integers representing the same coefficient of the 32 polynomials. Thus, we can do 32 polynomials computation at once.

This bitslicing transformation can be seen as a transposition of the original 32x8 bit matrix, which is a linear operation in \(GF(2)^N\) (this is important for what’s next).

Understanding the share format

The sss library’s README explains a little bit what happens in the sss_create_shares function. Basically, a random 32-bytes key \(K\) is computed, then used to encrypt and authenticate the original secret \(S\) with libsodium’s crypto_secretbox function. The rational behind this is explained in the aforementioned README.

The SSS algorithm is then applied on the key \(K\), creating in our case three shares. The share values can then be used in the sss_combine_shares, which recovers the key \(K\), and uses libsodium’s crypto_secretbox_open to verify the integrity of the encrypted data and recover the original secret \(S\).

Regarding the share format, analyzing the library’s source code teaches us that the result of the Authenticated Encryption with Associated Data (AEAD) of \(S\) with \(K\) is concatenated to every share. Moreover, each share, at its beginning, have its share index encoded in one byte.

So, the final format of a share is:

• First byte: share index (from 1 to 3 in our case)
• Next 32 bytes: the actual share value (representing the 32 polynomials)
• Remaining bytes: basically the output of crypto_secretbox, that encrypts & authenticate our original secret \(S\) with the random key \(K\)

What we got from the server is a Base64 encoding of this. If we indeed take a closer look at the two shares we received, we can see that the last bytes are the same.

The problem to solve

With all these information, we can say that the problem to solve can be summarized as such:

• given two known shares \((KS_1,KS_2)\) (among the original three shares \((KS_0,KS_1,KS_2)\)) of a secret (in our case the encryption key \(K\))
• and given the function \(F(K) = (KS_0,KS_1,KS_2)\),

can we retrieve \(K\) by only having \((KS_1,KS_2)\)?

Note: Once we got \(K\), we just need to use libsodium to retrieve the original secret \(S\).

Bibliography

This challenge has a very strong resemblance to this recent blog post, and given that Jean-Baptiste Bédrune is now head of security of the Ledger’s Donjon, this might not be just a coincidence :)

Figuring out the vulnerability

In theory, if SSS is properly implemented, that it isn’t possible to recover this secret with only two shares out of the three. So there must be some kind of vulnerability in the implementation of this scheme.

We can notice that a customized version of the sss library has been used. If we look at the differences, we can see that the major ones are in the randombytes.cpp file. Here is part of its implementation:

#define RANDOM_POOL_SIZE 128
static uint8_t random_pool[RANDOM_POOL_SIZE];

void randominit(void *entropy, size_t size) {
  sgx_sha256_hash_t digest;
  
  uint8_t *p = random_pool;
  sgx_sha256_msg((uint8_t *) entropy, (uint32_t) size, &digest);

  for (int i = 0; i < 4; i++) {
    memcpy(p, digest, SGX_SHA256_HASH_SIZE);
    sgx_sha256_msg(p, SGX_SHA256_HASH_SIZE, &digest);
    p += SGX_SHA256_HASH_SIZE;
  }
}

int randombytes(void *buf, size_t n) {
  if (n == 0) {
    return 0;
  }  

  uint8_t *data = (uint8_t *)buf;
  while (n > RANDOM_POOL_SIZE) {
    memcpy(data, random_pool, RANDOM_POOL_SIZE);
    data += RANDOM_POOL_SIZE;
    n -= RANDOM_POOL_SIZE;
  }  
  memcpy(data, random_pool, n); 
  return 0;
}

One issue here is that the randombytes function will always return the same bytes (looping over a buffer of 128 bytes). This means that, if we call twice the randombytes function to get, say, 32 bytes, we get twice the same random 32 bytes. Let’s see where this is used and how we can exploit this.

Constant randomness usage

Usage 1

The first place where randombytes is used is sss_create_keyshares. The randombytes function is thus used to compute the 32-bytes key that encrypts the data to share (see above).

void sss_create_shares(sss_Share *out, const unsigned char *data,
                       uint8_t n, uint8_t k)
{
  // ...
  unsigned char key[32];
  /* Generate a random encryption key */
  randombytes(key, sizeof(key));

  /* AEAD encrypt the data with the key */
  memcpy(&m[crypto_secretbox_ZEROBYTES], data, sss_MLEN);
  crypto_secretbox(c, m, mlen, nonce, key);

  /* Generate KeyShares */
  sss_create_keyshares(keyshares, key, n, k);

Usage 2

The next place where randombytes is used is in sss_create_keyshares in order to generate the various set of polynomials involved:

void
sss_create_keyshares(sss_Keyshare *out,
                      const uint8_t key[32],
                      uint8_t n,
                      uint8_t k)
{
  // ...
  uint32_t poly0[8], poly[k-1][8];

  /* Put the secret in the bottom part of the polynomial */
	bitslice(poly0, key);

  /* Generate the other terms of the polynomial */
  randombytes((void*) poly, sizeof(poly));
  //...
}

In our case, \(k\) (number of shares needed to retrieve the secret) is three, as long as \(n\) (number of total shares). We thus have 3 sets of 32 polynomials with coefficients in \(GF(2^8)\):

• one \(P_0\) set, which is the key \(K\)
• two other ones \((P_1,P_2)\), which are chosen randomly using randombytes.

With all these informations, let’s refine a little bit our problem to solve.

The refined problem to solve

As the representation of a set of 32 polynomials is composed of 32 8-bit integers (which means 32 bytes), due to the vulnerability explained above, this means that the first set of polynomials’ coefficients are directly tied to the 32-bytes random key \(K\).

This means that, from the description of the problem we gave above, we can refine the problem as such:

• with \(F\) a function that, given \((K,P_2)\), generates \((KS_1,KS_2)\), the problem is, knowing \((KS_1,KS_2)\), to retrieve \((K,P_2)\).
• stated differently, we want to solve the equation \(F(K,P_2) = (KS_1,KS_2)\) (knowing \((KS_1,KS_2)\)).

We can also note that \((K,P_2)\) is \(32+32=64\) bytes, as well as \((KS_1,KS_2)\). Let’s now take a closer look at \(F\).

Analyzing F

We can split the code of the sss_create_keyshares function, so that our function \(F\) becomes more explicit:

extern "C" void
sss_create_keyshares_impl(sss_Keyshare *out,
    const uint8_t key[32],
    const uint32_t* poly,
    uint8_t n,
    uint8_t k)
{
  uint8_t share_idx, coeff_idx, unbitsliced_x;
  uint32_t poly0[8], x[8], y[8], xpow[8], tmp[8];

  /* Put the secret in the bottom part of the polynomial */
  bitslice(poly0, key);

  for (share_idx = 0; share_idx < n; share_idx++) {
    /* x value is in 1..n */
    unbitsliced_x = share_idx + 1;
    out[share_idx][0] = unbitsliced_x;
    bitslice_setall(x, unbitsliced_x);

    /* Calculate y */
    memset(y, 0, sizeof(y));
    memset(xpow, 0, sizeof(xpow));
    xpow[0] = ~0; 
    gf256_add(y, poly0);
    for (coeff_idx = 0; coeff_idx < (k-1); coeff_idx++) {
      gf256_mul(xpow, xpow, x); 
      gf256_mul(tmp, xpow, &poly[coeff_idx*8]);
      gf256_add(y, tmp);
    }   
    unbitslice(&out[share_idx][1], y); 
  }
}

void
sss_create_keyshares(sss_Keyshare *out,
                      const uint8_t key[32],
                      uint8_t n,
                      uint8_t k)
{

  uint32_t poly[k-1][8];
  /* Generate the other terms of the polynomial */
  randombytes((void*) poly, sizeof(poly));

  sss_create_keyshares_impl(out, key, &poly[0][0], n, k); 
}

In this code, \(F\) is sss_create_keyshares_impl, called with n=3 and k=3. Moreover, due to the previously exposed issue the 32 bytes of key are the sames as the first 32 bytes of polys. This function basically implements the SSS protocol. As seen before, it’s using sets of 32 polynomials with coefficients in the \(GF(2^8)\) space.

As discussed in Annex A, multiplications by constant polynomials and additions in \(GF(2^8)\) can also be represented as linear functions in the \(GF(2)^8\) space. This can help us tell that the function \(F\) is linear in the \(GF(2)^{512}\) space.

Indeed, let’s take a closer look at the computation of one byte of the \(i\)-th share. This is basically evaluating a polynomial \(A\) of degree \(k-1=2\) (with coefficients \(a_i\) in \(GF(2^8)\)) in \(i\). With \(C_i\) the polynomial representation of \(i\) in \(GF(2^8)\) (e.g. here with \(i=3 \implies C_i = 1+x\)): \[\begin{align*} A(C_i) &= a_0 + a_1*C_i + a_2*C_i^2 \\ &= a_0 + a_1*(1+x) + a_2*(1+x)^2 \\ &= a_0 + a_1*(1+x) + a_2*(1+x^2) \\ &= (a_0+a_1+a_2) + a_1*x + a_2*x^2 \end{align*}\]

With \(a_i = \sum_{j=0}^{7} (b_{i,j}*x^j)\), we end up with a polynomial in \(GF(2^8)\), whose coefficients are linear combinations of \((b_{ij})\). So, for this specific share, we can rewrite this operation in \(GF(2)^{8*3}\) as: \[M_i\times\begin{pmatrix}b_{0,0} \\ b_{0,1} \\ \dots \\ b_{0,7} \\ b_{1,0} \\ \dots \\ b_{2,7} \end{pmatrix}\]

with \(M_i\) a \(24 \times 8\) bit matrix.

Moreover, as said above, the bitslicing part is just an optimisation, and can also be seen as a linear function. We can notice that the sss_create_keyshares_impl takes “unbitsliced” inputs, and returns “unbitsliced” outputs. So, in the end, we don’t really have to take care about this internal representation and optimisation.

Finally, we can say that our problem basically boils down to solving a linear system in \(GF(2)^{512}\)! What we miss is the representation of \(F\) in that space.

Note: we don’t necessary need to precisely understand all these things to solve the challenge. We can make the assumption that \(F\) will be linear in the \(GF(2)^{512}\) vector space, and quickly try if that’s the case (see the provided source code for an example).

Exploiting the vulnerability (and solving the challenge)

Let’s recap what we have to do:

• we know the key shares \((KS_1,KS_2)\), which are both 32-bytes long
• we have the function \(F\), which can be represented as a linear function in the \(GF(2)^{512}\) vector space. We have the code of that function, so we can evaluate it
• we have to retrieve the original secret by solving the equation \(F(K,P_2) == (KS_1,KS_2)\)

As \(F\) is a linear function in \(GF(2)^{512}\), it can be represented by a 512 square bit matrix \(M\). Remember, \(GF(2)\) basically means \(\{0,1\}\) (it’s a bit), and the size of \((K,P_2)\) and \((KS_1,KS_2)\) is 64 bytes.

So, in the end, we want to solve this equation: \[M\times\begin{pmatrix}K \\ P_2\end{pmatrix} = \begin{pmatrix}KS_1 \\ KS_2\end{pmatrix}\]

Note that \(M\) might not be invertible, so it might not be “as simple” as writing the inverse of \(F\) and compute it.

Computing \(M\) using DragonFFI

One thing that remains is to compute the matrix \(M\). There are basically two ways to do this:

• compute the matrix by hand, by composing all the various operations that are happening in \(F\). This is a bit time consuming and potentially error-prone.
• evaluate \(F\) 512 times to compute the values of the column of \(M\). Indeed, if, for every column index \(i\) of \(M\), we compute \(F(V)\), with V a bit vector with only the \(i\)-th index at 1 (and the others at zero), then we directly get the vector of the column \(i\) of \(M\).

Let’s go for the second option, and do that using DragonFFI to directly call sss_create_keyshares_impl from Python:

import pydffi
FFI=pydffi.FFI()
CU=FFI.cdef('''
#include <stdint.h>
void sss_create_keyshares_impl(uint8_t *out,
  const uint8_t* key,
  const uint8_t* poly, // was uint32_t*
  uint8_t n,
  uint8_t k);
''')

def polys_to_keyshares(polys):
    assert(len(polys) == LEN_POLYS)
    # This is due to the random generator reusing the same data (this is the vuln we are exploiting).
    key = polys[:LEN_KEY]
    out = bytearray([0]*LEN_KEYSHARES)
    CU.funcs.sss_create_keyshares_impl(out, key, polys, NSHARES, NSHARES)
    ret = (out[:LEN_KEYSHARE], out[LEN_KEYSHARE:2*LEN_KEYSHARE], out[2*LEN_KEYSHARE:])
    return ret

def kss_to_F_output(kss):
    return kss[1][1:] + kss[2][1:]

# This is our function F. It takes 64 bytes as input (two polynoms), and
# returns the last two shares (2*32 bytes)
def F(in_):
    kss = polys_to_keyshares(in_)
    return kss_to_F_output(kss)

# We work with vector of bits, so we choose a way to transform a list of bytes
# into a list of bits and vice versa. Any representation would work, as long as
# bytes2bits is the inverse of bits2bytes. Implementation is in the provided
# source code.
def bits2bytes(v):
  # ...

def bytes2bits(v):
  # ...

from sage.all import Integers, Matrix, vector
GF2=Integers(2)
def computeFMatrix(F, input_nbits):
    ret_cols = []
    for bin_ in range(input_nbits):
        in_ = [0]*NBITS
        in_[bin_] = 1
        in_ = bits2bytes(in_)
        out = F(in_)
        out = bytes2bits(out)
        ret_cols.append(out)
    return Matrix(GF2, ret_cols).transpose()
NBITS=64*8
M=computeFMatrix(F, NBITS)

Solving the problem with sage

Now that we got the matrix, it’s a matter of asking Sage to solve the problem for us.

The first thing we can verify is the size of the kernel of \(M\), that is the number of vector \(X\) for which \(M \times X == 0\). This will basically gives us the number of possible solutions to the problem:

print(M.kernel())

which gives:

Vector space of degree 512 and dimension 2 over Ring of integers modulo 2
Basis matrix:
2 x 512 dense matrix over Ring of integers modulo 2

As the dimension of the result vector space is \(2\), we will have \(2^2 = 4\) potential solutions, which is fine to bruteforce :)

Now, let’s ask Sage to finally solve this:

# Get all possible values of X in M*X = C thanks to Sage
def allsols(M, C):
    S0 = M.solve_right(vector(GF2,bytes2bits(C)))
    for S in M.right_kernel():
        yield S + S0

# We extract the two shares from the mails we received
Fout = shares[2]+shares[3]
keys = []

for S in allsols(M, Fout):
    S = [int(v) for v in S]
    # The solution will give us the encryption K and the polynom P2. We only
    # care about K here.
    key = bits2bytes(S)[:32]
    print("[x] Possible key: %s" % key.hex())
    keys.append(key)

Recovering the original private key

Last part is to bruteforce these 4 keys and retrieve the original secret:

for k in keys:
    out = bytearray([0]*64)
    # sss_decrypt is basically a wrapper around crypto_secretbox_open
    # added to the sss lib (source code in the provided repository)
    if int(CU.funcs.sss_decrypt(out, msg, k)) == 0:
        print("[+] Original secret found: %s" % out.hex())
        sys.exit(0)

To get the flag, we just had to give the found secret to a script that would verify that it is indeed the private key associated to the challenge’s wallet public key, and output the flag as CTF{secret_in_hex}:

  $ python ./check_flag.py 7d486b4cfdb1ede284802029e77ab292c35ab0d7b9d8c51a06b9222e5095e98c
  CTF{7d486b4cfdb1ede284802029e77ab292c35ab0d7b9d8c51a06b9222e5095e98c}

And that’s it!

Conclusion

That was a very nice challenge, which showcases how a simple vulnerability in a random generator can break an apparently well designed system!

Acknowledgment

Thanks to ssp for reviewing this writeup at 11PM, and the Donjon Ledger team for this CTF!

Annex A: \(GF(2^N)\) versus \(GF(2)^N\)

This annex explains why some operations in \(GF(2^N)\) can be represented as linear operation in the vector space \(GF(2)^N\) (which means a vector space using vectors of N bits).

\(GF(2^N)\) represents polynomials with coefficients in \(GF(2)\) (aka a bit). For instance, for \(N = 8\): \(P(x) = a_0 + a_1*x + a_2*x^2 + ... + a_7*x^7\). As each coefficient is a bit, we can also represent them as bits. Let’s call that representation bits(P).

Additions and multiplications are the usual ones. Addition of two polynomials A and B gives: \[A(x) + B(x) = (a_0+b_0) + (a_1+b_1)*x + ... + (a_7+b_7)*x^7\]

As coefficients are in \(GF(2)\), the addition can be seen as a simple XOR operation. This means that \(A+B\) == poly(bits(A)^bits(B)). With \(BA\) and \(BV\) in \(GF(2)^8\), this also means that this polynomial addition can also be represented as a simple \(BA + BV\) vector addition in this vector space.

Multiplications in \(GF(2^N)\) are reduced to a fixed polynomial. Multiplying a unknown polynomial \(X\) with a known polynomial \(C\) can also be represented as a linear operation \(M_C \times X\) in \(GF(2)^N\) (with \(M_C\) an NxN bit matrix). Let’s just take an example to give the intuition behind this, with \(N = 4\), \(C = 1+x^2\), and \(x^4 + x + 1\) the reduction polynomial: \[\begin{align*} A(x)*C &= (a_0+a_1*x+a_2*x^2+a_3*x^3)*(1+x^2) \\ &= a_0 + a_1*x + (a_2 + a_0)*x^2 + (a_3 + a_1)*x^3 + a_2*x^4 + a_3*x^5 \end{align*}\]

Reduced \(\pmod{x^4 + x + 1}\), we have \[\begin{align*} x^4 &= x + 1 & \pmod{x^4 + x + 1}\\ x^5 &= x^2 + x & \pmod{x^4 + x + 1} \end{align*}\]

Which gives us: \[\begin{split} &A(x)*C \pmod{x^4 + x + 1} \\ & = a_0 + a_1*x + (a_2 + a_0)*x^2 + (a_3 + a_1)*x^3 + a_2*(x + 1) + a_3*(x^2 + x) \\ & = (a_0 + a_2) + (a_1 + a_2 + a_3)*x + (a_0 + a_2 + a_3)*x^2 + (a_1 + a_3)*x^3 \end{split}\]

If we model \(A\) as a 4-bit vector in \(GF(2)^4\), we can represent \(A(x)*C\) as a linear operation \(M_C \times A\), with \(M_C\) a 4x4-bit matrix: \[\begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \end{pmatrix}\]